Só para recapitular, os números primos são aqueles que são divisíveis somente por eles mesmos e por 1. Nenhum número par (exceto 2) pode ser primo, porque todos os pares podem ser divididos por 2. Mas 3 é primo, e 19 também é primo, por exemplo, porque não tem como dividir eles por qualquer outro número além deles mesmos e 1. Já se sabe que os números primos são infinitos, e agora vou explicar porque eles também são misteriosos e fascinantes.
Não existe até hoje alguma fórmula capaz de agrupar todos os primos. Ainda é impossível prever quando o próximo primo vai aparecer, às vezes eles estão separados por mais de mil números e às vezes eles estão separados apenas por um número – e esses são conhecidos como números primos gêmeos – estamos ainda totalmente perdidos, e para nós parece que eles se comportam de maneira aleatória.
Por exemplo, essa figura mostra a distribuição de gotas de chuva aleatórias, representadas pelas linhas de cima, e embaixo está a distribuição de cem números primos.

Não tem nem como imaginar qual das duas linhas mostra os números primos e qual mostra as gotas de chuva. Mas sabemos que a distribuição dos primos, apesar de parecer aleatória, não o é, o que acontece é que ainda não conseguimos ver qualquer harmonia nela. Isso é muito misterioso!
É incrível que ainda seja impossível encontrar um padrão que mostre a localização dos primos. Ainda mais se pararmos para pensar que esses números simplesmente são base para qualquer outro número. Eles são os blocos de construção dos outros números, já que qualquer número pode ser gerado a partir da multiplicação de primos.
A Hipótese de Riemann
Em 1859, o matemático alemão Bernard Riemann fez uma hipótese que, mesmo tendo surgido mais de 150 anos atrás, continua sendo o principal avanço em direção a uma ordem no caótico mundo dos primos. Sei que não vai dar para entender assim em um parágrafo, porque é supercomplexa e envolve muitos cálculos, e eu também não entendo bem, mas basicamente a hipótese de Riemann diz que existe uma fórmula chamada função zeta de Riemann, essa fórmula determina um gráfico de quatro dimensões, formado pelos números naturais e pelos os números imaginários. Riemann propôs que todos os zeros não-triviais (os zeros formados por números naturais positivos) que surgirem como resultado dessa fórmula estariam sempre agrupados sobre a mesma linha. E essa localização dos zeros está intimamente conectada com a localização dos números primos.
O problema é que até agora ninguém conseguiu provar a hipótese de Riemann, principalmente porque os zeros – assim como os números primos – são infinitos. E temos que achar cada zero, um por um, assim como fazemos com os números primos. Até agora já foram encontrados 6,3 bilhões de zeros sobre a linha, e nenhum fora dela. Mesmo assim ainda não é possível garantir que a hipótese seja verdadeira. Sem que descubramos uma maneira de prever a localização de todos os zeros, é impossível provar que todos eles estejam sobre a mesma linha.
Abaixo estão três representações da função zeta de Riemann, as três são muito diferentes, provavelmente porque a paisagem da função zeta tem quarto dimensões, então existem milhares de fatias e recortes possíveis para reduzi-la a duas ou três dimensões, para que se torne visual para nós.

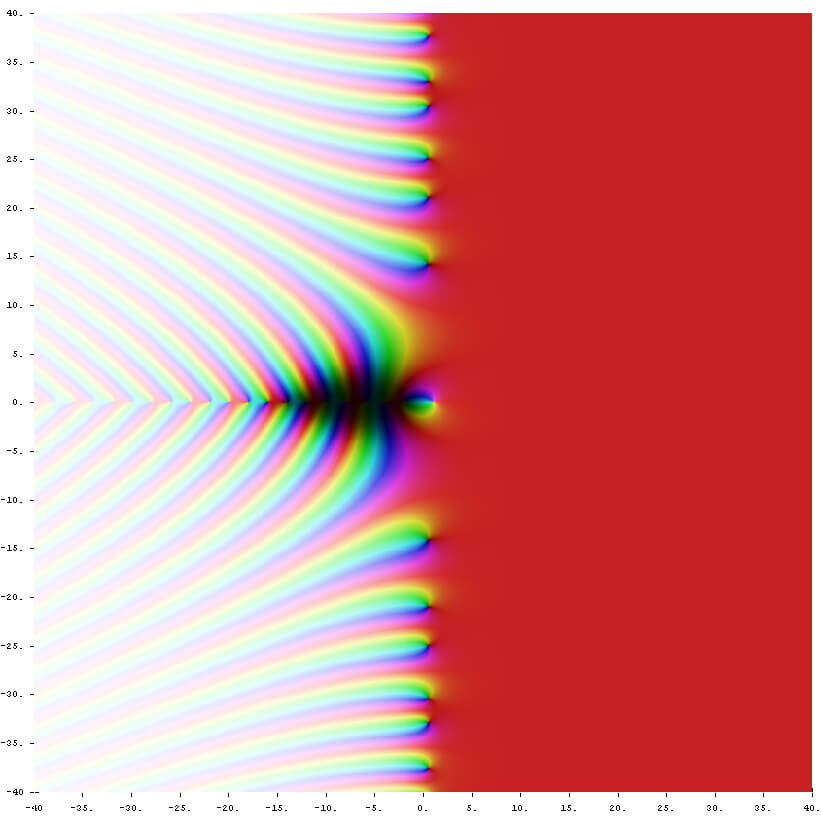
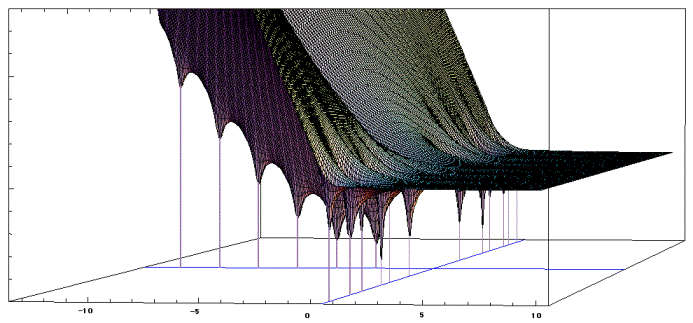
Existe um prêmio de um milhão de dólares a ser entregue para qualquer pessoa que consiga provar a hipótese de Riemann, esse é atualmente o problema mais misterioso da matemática.
Alan Turing também se apaixonou pelos primos, e achou que com a invenção dos computadores seria mais fácil desvendar a hipótese de Riemann, mas os computadores só ajudam a encontrar o próximo primo, o próximo zero sobre a linha crítica. Agora existem comunidades inteiras dedicadas a procurar números primos enormes, gigantes. O maior até agora tem mais de 22 milhões de dígitos. Chega a ser absurdo pensar que existe um número tão grande e que ainda assim não possa ser quebrado em dois números menores, que é um bloco inteiro e indivisível. De qualquer forma a chegada dos computadores não ajudou a encontrarmos um padrão, para isso teríamos que mudar a maneira de enxergar esse problema, teríamos que olhar para os primos de uma forma completamente nova.
Por exemplo, uma das novas vertentes de pesquisa faz uma conexão entre a teoria dos números e a física e acredita que todos os zeros estão sobre a mesma linha porque eles obedecem as frequências de uma espécie de “tambor matemático”, exatamente como os elétrons só podem orbitar determinadas órbitas preestabelecidas e não o espaço entre elas.

Recentemente aconteceu um grande avanço em direção a descoberta de um padrão nos primos: uma dupla de pesquisadores conseguiu provar que a distribuição dos primos não é aleatória.
Eles provaram, a partir do fato de que os primos só podem terminar em 1, 3, 7 ou 9, que existe uma exata probabilidade de que o próximo primo termine em cada uma dessas possibilidades, por exemplo, um primo terminado em 1 tem 18% de chance de ser seguido por outro primo terminado em 1, 30% de chance de ser seguido por um primo terminado em 3 ou 7 e 22% de chance de ser seguido por um primo terminado em 9. Parece pouco em direção à um vislumbre de padrão, e é mesmo. Mas pelo menos agora temos certeza que eles não são aleatórios, já que se eles fossem aleatórios todos teriam exatamente 25% de chance de aparecerem depois de qualquer opção. Sobre sua descoberta, Lemke Oliver, um dos responsáveis pela pesquisa disse que “o que sabemos até agora é vergonhosamente pouco”.
Criptografia
Por serem tão imprevisíveis, os primos servem de base para o algoritmo de criptografia RSA, que hoje é usado em muitos lugares da internet para garantir a segurança de transações com cartão de crédito ou qualquer compra online.
No sistema RSA cada compra recebe um número imenso, que só pode ser quebrado se dividido por dois números primos, cada um com mais de cem algarismos. E só existe uma maneira, só existe um único par de primos capaz de formar esse imenso número-chave. E como não existe nenhuma fórmula capaz de encontrar rapidamente esses primos imensos, os computadores que queiram interceptar essa compra (e roubar os dados do cartão de crédito, por exemplo) teriam que tentar todas as combinações de primos possíveis, uma por uma, e isso levaria muito tempo. Não existe atalho. Por isso o sistema de criptografia RSA é tão eficaz.
Primos na Natureza
Os primos aparecem em vários locais da natureza – temos 23 pares de cromossomos, as estrelas marinhas têm 5 pontas, etc. Mas o mais interessante é ver a escolha de sequências de primos como estratégia de sobrevivência, como acontece com as cigarras:
Existem duas espécies de cigarras chamadas Magicicada septendecim e Magicicada tredecim, que vivem no mesmo ambiente. As cigarras passam quase toda a vida enterradas, se alimentando de seiva de árvore, mas um pouco antes de morrerem elas emergem do solo para se reproduzirem. Essas duas espécies possuem ciclos de vida de 17 e de 13 anos, respectivamente, que são ambos primos. A escolha de números primos faz com que elas só tenham que dividir a floresta uma vez a cada 221 anos! Escolher números primos como ciclos de vida foi uma tática evolutiva superesperta. Além de garantir a floresta só para uma espécie por vez, ajuda a evitar predadores. O matemático, e apaixonado por números primos Marcus du Sautoy explica que “porque 13 e 17 são ambos indivisíveis, isso da às cigarras uma vantagem evolutiva, porque ajuda a evitar outros animais com comportamento periódico. Suponhamos que um predador apareça na floresta a cada 6 anos. Então uma cigarra com ciclo de vida de 8 ou 9 anos vai coincidir com o predador muito mais frequentemente do que uma cigarra com um ciclo primo de 7 anos”

O matemático francês Alain Connes acreditava que a matemática é “inquestionavelmente a única linguagem universal.” e que “podemos imaginar diferentes químicas ou biologias do outro lado do universo, mas os números primos continuarão sendo primos em qualquer galáxia que encontremos”. Mesmo assim, a harmonia por trás do distribuição dos primos continua sendo um dos maiores mistérios do mundo. O matemático norueguês Selberg disse uma vez que “talvez, contudo, a prova [da hipótese de Riemann] seja tão intrincada que o cérebro humano não consiga abraçá-la”. E assim a lógica por trás dos números primos talvez esteja mesmo fora do nosso alcance, embasada pelo teorema da incompletude de Gödel, que diz que existem teorias que apesar de verdadeiras, jamais poderão ser provadas.
Essa é uma perspectiva triste. Mas talvez a beleza desses números venha justamente da sua natureza egoísta, em que cada um existe totalmente sozinho, sem divisor, sem ajudar em nada a prever onde estará o próximo, ou a compor uma paisagem maior do que a si próprio.
A principal fonte de pesquisa para esse texto foi o livro A música dos números primos, de Marcus du Sautoy.